初一数学辅导计划
总体目标
- 平稳过渡,适应新环境:帮助学生适应初中数学的学习节奏、难度和思维方式,克服从小学到初中的“陡坡”效应。
- 夯实基础,扫清障碍:系统梳理并巩固小学阶段的核心知识点,确保学生能熟练运用。
- 掌握核心,建立体系:深入理解并掌握初一上、下学期的核心概念(如有理数、整式、方程、几何初步等),构建初中数学的知识框架。
- 培养习惯,提升能力:引导学生养成预习、复习、反思的良好学习习惯,培养逻辑思维、空间想象能力和解题规范性。
- 激发兴趣,建立自信:通过趣味教学和成功体验,让学生感受数学的魅力,建立学好数学的自信心。
辅导对象分析
- 基础薄弱型:小学基础不牢,计算能力差,对数学有畏难情绪。
- 中等偏上型:基础尚可,但知识点掌握不系统,解题思路不清晰,综合运用能力不足。
- 拔高冲刺型:基础扎实,希望拓展思维,挑战更难题型,为竞赛或后续学习做准备。
(本计划将主要针对前两类学生,拔高型学生可在基础上增加拓展内容)
辅导原则
- 以课本为本,紧扣大纲:所有辅导内容必须围绕学校教材和教学大纲展开,确保与学校教学同步。
- 循序渐进,温故知新:从学生已有知识出发,逐步引入新概念,做到“新中有旧,旧中有新”。
- 讲练结合,注重实效:精讲多练,每学习一个知识点,立即配备针对性练习,及时巩固。
- 启发引导,而非灌输:多提问、多引导,鼓励学生独立思考,培养其主动解决问题的能力。
- 鼓励为主,建立信心:及时发现学生的闪光点和进步,给予积极肯定,保护其学习热情。
辅导内容与进度安排(以人教版为例)
第一阶段:入门与适应期(约1-2个月,覆盖初一上学期前半段)
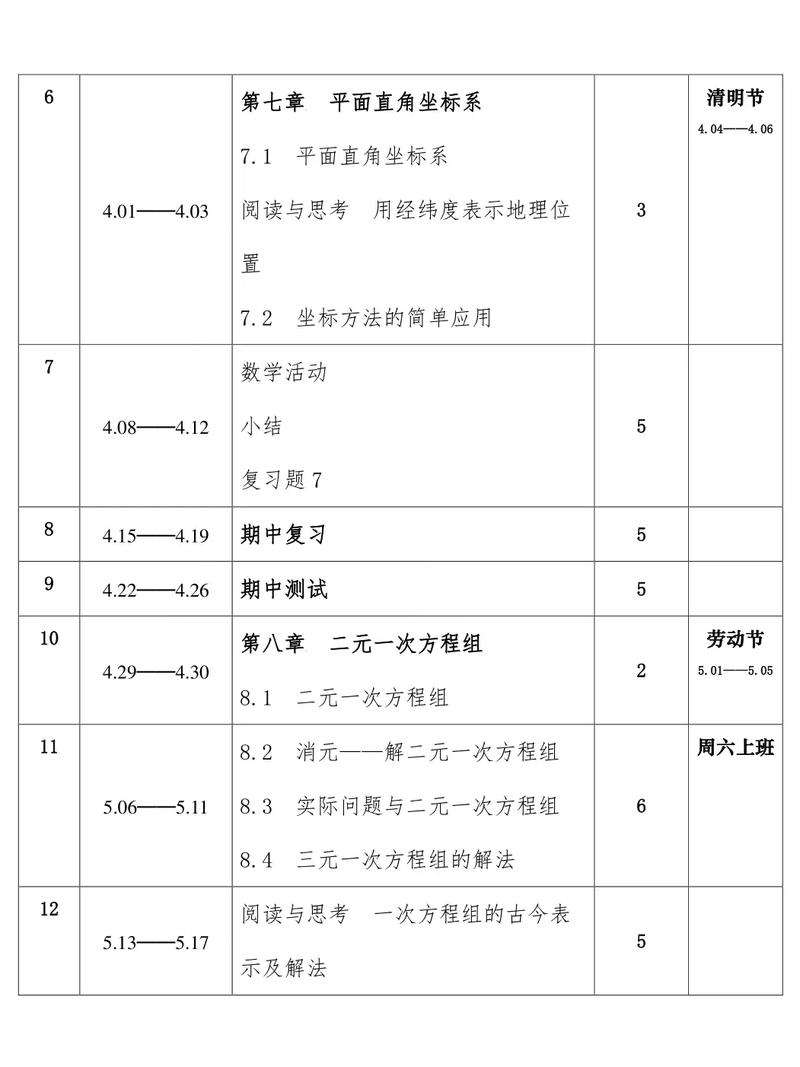
| 模块 | 核心知识点 | 辅导重点与难点 | 建议课时 | 辅导方法 |
|---|---|---|---|---|
| 有理数 | • 正数与负数 • 数轴、相反数、绝对值 • 有理数的加减乘除运算 • 有理数的混合运算 |
重点:数轴的理解与应用,绝对值的非负性,四则运算的法则。 难点:绝对值的化简,混合运算的符号判断和运算顺序。 |
8-10课时 | 可视化教学:用数轴模型动态演示加减法。 口诀记忆:总结有理数运算口诀。 错题精讲:针对常见运算错误进行专项训练。 |
| 整式的加减 | • 单项式、多项式、系数、次数 • 同类项 • 合并同类项 • 去括号与添括号法则 |
重点:准确判断同类项,熟练运用合并同类项和去括号法则。 难点:去括号时符号的变化,整式化简求值的步骤。 |
4-6课时 | 类比法:将同类项比作“同类水果”,合并同类项比作“装水果”。 步骤化训练:强调“先去括号,再合并同类项”的规范步骤。 |
| 一元一次方程 | • 方程、解方程的概念 • 等式的性质 • 解一元一次方程的步骤(移项、合并、系数化为1) • 实际问题与一元一次方程(和差倍分、行程、工程等) |
重点:解方程的步骤,寻找等量关系。 难点:应用题中等量关系的分析,设未知数的技巧。 |
6-8课时 | 建模思想:引导学生将实际问题抽象为数学方程。 “找等量关系”专项训练:通过画线段图、列表格等方式帮助学生分析。 一题多解:鼓励学生尝试不同的设未知数方法。 |
第二阶段:巩固与深化期(约2-3个月,覆盖初一上学期后半段及下学期前半段)
| 模块 | 核心知识点 | 辅导重点与难点 | 建议课时 | 辅导方法 |
|---|---|---|---|---|
| 几何图形初步 | • 直线、射线、线段 • 角的概念与度量 • 余角和补角 • 相交线与平行线(初步) • 基本作图 |
重点:线段和角的基本概念、性质和计算。 难点:几何语言的理解与表达,平行线的性质与判定(初步)。 |
6-8课时 | 直观教学:大量使用实物、模型和画图工具。 规范作图:严格要求使用作图工具,培养严谨的几何习惯。 图形变换:通过动态演示理解角、线的平移和旋转。 |
| 相交线与平行线 | • 垂直、对顶角 • 同位角、内错角、同旁内角 • 平行线的判定与性质 • 平行线的证明(初步) |
重点:平行线的三个判定和三个性质。 难点:性质与判定的区别与联系,简单的逻辑推理证明过程。 |
6-8课时 | 对比学习:制作表格,对比“判定”和“性质”的条件和结论。 逻辑链条:引导学生写出“∵...∴...”的规范推理过程。 变式训练:通过改变图形条件,让学生灵活运用知识。 |
| 实数 | • 平方根、算术平方根 • 立方根 • 实数的概念与分类 • 实数的数轴表示与大小比较 |
重点:平方根与算术平方根的区别与联系,无理数的概念。 难点:理解无理数的存在,实数范围内的运算。 |
4-6课时 | 数形结合:在数轴上画出√2等无理数,感受实数的连续性。 概念辨析:通过对比练习,区分平方根、算术平方根、立方根。 |
| 平面直角坐标系 | • 坐标系的构成 • 点的坐标的确定与描点 • 各象限及坐标轴上点的坐标特征 • 用坐标表示平移 |
重点:点的坐标与位置的对应关系。 难点:理解平移前后坐标的变化规律。 |
3-4课时 | 游戏化教学:“寻宝游戏”,根据坐标找点。 动态演示:使用动画展示图形平移时坐标的变化。 |
| 二元一次方程组 | • 二元一次方程(组)的概念 • 代入消元法、加减消元法 • 实际问题与二元一次方程组 |
重点:掌握两种消元法解方程组。 难点:选择合适的消元方法,复杂应用题的等量关系分析。 |
6-8课时 | 方法对比:对比代入法和加减法的优缺点,让学生根据题目特点自主选择。 “消元”思想:强调解方程组的核心思想是“化二元为一元”。 |
第三阶段:总复习与提升期(考前及期末)
- 知识梳理:带领学生绘制本学期(或学年)的思维导图,将零散的知识点串联成网,形成知识体系。
- 专题复习:
- 计算专题:有理数、整式、方程的综合计算,强调准确性和速度。
- 几何证明专题:平行线的综合证明题,训练逻辑推理能力。
- 应用题专题:行程、工程、浓度、利润等经典应用题的解题策略。
- 模拟测试:进行2-3套模拟卷测试,严格按照考试时间,进行实战演练。
- 错题回顾:重点分析学生之前练习和测试中的错题,查漏补缺,确保同样的错误不再犯。
辅导方法与策略
- 课前预习:每次辅导前,让学生提前浏览下节课要讲的内容,带着问题来上课。
- 互动式教学:多采用提问、讨论、让学生上台讲解等方式,避免“一言堂”。
- “一题多解”与“多题一解”:
- 一题多解:开阔学生思路,培养发散思维。
- 多题一解:归纳总结同类题型的通用解法,举一反三。
- 建立“错题本”:要求学生整理错题,并写下错误原因和正确思路,定期回顾错题本,效果显著。
- 正向激励:对学生的每一点进步都给予表扬,可以用小星星、积分等方式,兑换小奖品或特权,激发学习动力。
辅导效果评估
- 过程性评估:通过课堂提问、课堂练习、作业完成情况,实时了解学生掌握程度。
- 阶段性评估:每个模块结束后进行一次小测验,检验学习成果。
- 终结性评估:以学校期中/期末考试成绩为主要评估标准,对比辅导前后的成绩变化。
- 综合能力评估:观察学生的学习习惯、解题规范性、逻辑表达能力是否有提升。
温馨提示:
- 家校沟通:定期与家长沟通学生的学习情况和心理状态,形成教育合力。
- 劳逸结合:辅导时间不宜过长,注意学生的休息,避免疲劳战。
- 保持耐心:对于基础薄弱的学生,要有足够的耐心和爱心,允许他们犯错和反复。
这份计划是一个通用模板,具体实施时,需要根据学生的具体情况(如接受能力、薄弱环节、学校教学进度等)进行灵活调整和个性化定制,祝辅导顺利成功!